Elligno Inc.

Elligno Inc. (Scientific Simulation Framework)

Project: Over the last 5 years we have been implementing (programming) different application for physics  modeling and scientific computing using Object-Oriented Numeric. Particularly, a scientific simulation framework, organized in libraries that can be easily extended to accelerate the development of physics simulator. The main application is in the field of Open Channel Flow is called DamBreak++. It’s a plug-in library designed such as it can be easily to program new numerical algorithm to be validating on the dam-break problem. The overall of the software project is to provide rapid prototyping environment in physical modeling which include a Physics 3D library for the simulation of rigid-body featuring a Math 3D library for efficient floating-point operation on mathematical abstraction.

Technologies: C++, OO, UML, ODE (physics library), NR in C++, OSG, Boost, STL, Qt;

Numerical Modeling of Shock Wave Propagation (dam-break problem)

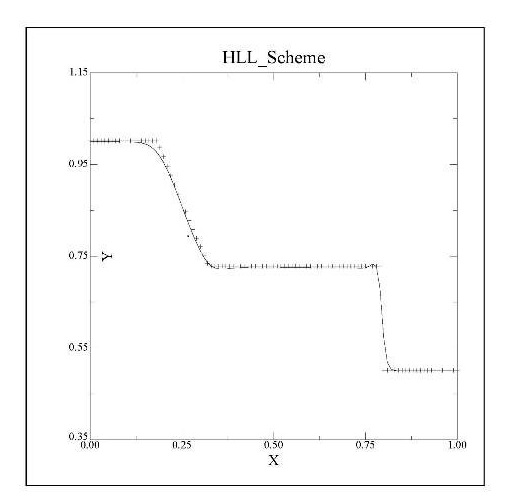
A semi-discrete scheme of second-order in time and space (finite volume model) based upon finite-difference grid is used for solving shallow water equations. The model performs time stepping by a Runge-Kutta solver  that uses a predictor/corrector method. The fluxes are calculated based on a Riemann solver of type HLL (Harten-Lax-van Leer). A simple TVD scheme is employed for shock capturing purposes in which the Minmod limiter is used for flux functions. In the figure below we can see the profile of the shock wave propagation (shock-wave). The numerical solutions are compared with analytical results. The errors from the analytical solutions are estimated and presented.