Scientific Simulation Framework
Introduction
This scientific programming environment project was initiated many years ago aimed at understanding physics via modern modeling techniques and using new software development paradigms. Efforts are focused on reusability and extensibility of software components. The main objective is to dramatically reduce the time needed to program/implement physical algorithm with a minimum effort and using little coding.
Motivation
Accelerate the prototyping phase in the validation of numerical algorithm on the so-called Dam Break problem in industrial projects. The physicist is often called to test or experiment with different scenarios, this type of environment meets this need.
Scientific Simulation System (SFX)
The Finite Difference Framework
This framework implemented within first-version software still undergoing development, contains basic building blocks to solve numerically the One-dimensional St-Venant equations corresponding to the explicit finite difference scheme.
Mathematical Model and Numerical Method
Dam-Break Problem
Physics Modeling Of The Dam-Break Problem (Non-Linear Wave Propagation)
The dam break problem in a horizontal channel is a classical problem in fluid mechanics and is motivated by numerous applications in environment and industrial processes. In this problem, a rectangular column of water, in hydrostatic equilibrium, is confined between two walls. Gravity is acting downwards with a magnitude of -9.81 m/s2. At the beginning of the calculation, the right wall is removed and the water is allowed to flow out to the horizontal wall. This classical test case is considered a benchmark for comparison of the performance of numerical schemes (numerical stability) specially designed for discontinuous transient flow, namely its non-linearity can give rise to discontinuous solutions currently referred to as bores or jumps.
Simulation taken from the programming environment. The first figure (left to right) shows the initial water level profile at t=0.5 sec, just after removing the thin film separating the two columns of water. We can see the water starting to collapse. The next figure shows the different profile as the shock-wave propagating takes place at various times. A shock-capturing method (Riemann solver) is used. The last figure shows the final profile.
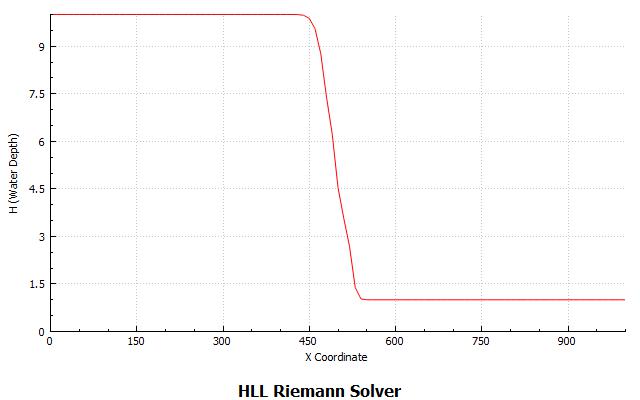
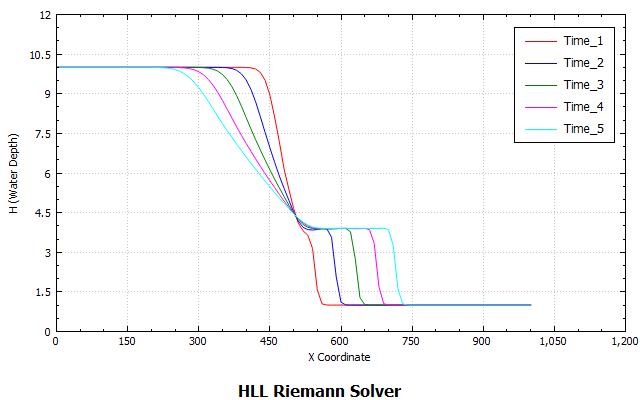
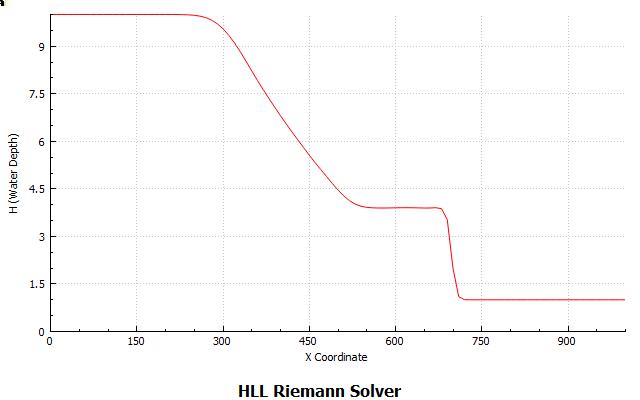
DamBreak++ API
Code snippet #1 (Building a physics simulator)
An example taken from our programming environment (DamBreak simulator)
...
// Now create the simulation environment that the user
// has defined using the appropriate factory methods
try
{
// Create a new Physical System Factory
std::cout << "Creating the physical system...\n";
PhysicalSystemFactory* w_PhySysF = PhysicalSystemFactory::getInstance();
physicalSystem = dynamic_cast<DamBreakSystem*>( w_PhySysF->create( w_globalDisscr));
g_pLogger->write2File( "PhysicalSystem created successfully");
std::cout << "created\n";
// Configure the objects in the physical system
std::cout << "Configuring system using < "
+ g_pSimulation->getPhysicalConfigurationClass() + ">...\n";
Class* setupClazz = Class::forName( g_pSimulation->getPhysicalConfigurationClass());
w_phyConfig = (IPhysicalConfiguration*)setupClazz->newInstance();
w_phyConfig->configure( physicalSystem);
g_pLogger->write2File( "PhysicalSystem configured successfully");
// Define the algorithm class to be used per iteration on the PhysicalSystem
std::cout << "Configuring Algorithm using < "
+ g_pSimulation->getPhysicalAlgorithmClass() + ">...\n";
Class* algorithmClazz = Class::forName( g_pSimulation->getPhysicalAlgorithmClass());
w_phyAlgo = (IPhysicalAlgorithm*)algorithmClazz->newInstance();
g_pLogger->write2File( "PhysicalAlgorithm created successfully");
// Define the measurement class to be used on the physical system
std::cout << "Configuring Physical Measurement using <" +
g_pSimulation->getPhysicalMeasurementClass() + ">...\n";
Class* measurementClazz = Class::forName( simulation.getPhysicalMeasurementClass());
physicalMeasurement = (IPhysicalMeasurement*)measurementClazz.newInstance();
g_pLogger->write2File("");
std::cout << "configured\n";
catch(...) // all exceptions
{
// to do: ....
}
};
...Code Snippet
In the code below, we use a solver of type HLL, belongs to Riemann solver, and interpolation procedure of state variables to compute flux. OON (Object-Oriented Numerics) makes it easy to program this kind of algorithm using basic types of the framework.
...
// const context variable
constexpr auto w_gravity = Sfx::PhysicalConstant::gGravity;
// compute gradient over each cell by applying a slope limiter function
// that belongs to family of TVD-Scheme (Total Variation Diminishing)
// modeling of sharp delta function (discontinuity)
std::function<float64(float64, float64)> w_minmodFunc = HydroUtils::minmod;
const auto w_dA = computeDU( U1, w_minmodFunc); // first state variable (A)
const auto w_dQ = computeDU( U2, w_minmodFunc); // second state variable (Q)
// retrieve computational domain (physics equation to be simulated)
const Omega& w_domain = GlobalDiscretization::instance()->omega();
// Create a list of global cell face (deprecated used for prototyping)
const auto& w_listFaces = createListGlobalFaces( w_domain.total_element_no());
auto begListFaces = w_listFaces.cbegin(); // initalize cell faces range
// Compute cell face flux j+1/2 (global faces) using Godunov-type scheme
while( begListFaces != w_listFaces.cend())
{
// 'cellFace' type is a representation of the cell interface (j+1/2)
const cellFace& w_cFace = *begListFaces++;
auto w_leftIdxNode = w_cFace.getLeftNodeI(); // stencil [i-1,i]
auto w_rightIdxNode = w_cFace.getRightNodeI(); // stencil [i,i+1]
// Calcul des éléments des vecteurs UR, UL, FR et FL
// (MUSCL extrapolation order of state variable at cell face)
Dsn::StateVector w_UL{ U1[w_leftIdxNode] + 0.5*w_dA[w_leftIdxNode], //A
U2[w_leftIdxNode] + 0.5*w_dQ[w_leftIdxNode] }; //Q
Dsn::StateVector w_UR{ U1[w_rightIdxNode] - 0.5*w_dA[w_rightIdxNode], //A
U2[w_rightIdxNode] - 0.5*w_dQ[w_rightIdxNode]}; //Q
...References
“An Extensible C++ Framework for One-Dimensional Open Channel Flow Simulation – J. Belanger (in preparation)
Abstract In this report we provide an introduction to ODE, then present an extensible Object-Oriented framework – written in C++ – with emphasis on the reusability of modules for ODE solvers. The ability to extend this API to accommodate new algorithms as they are developed is particularly attractive. This facilitates our work to find the best numerical method, and speed the development of a dedicated simulator for specific cases.
“A C++ Differential Equations Solver using Object-Oriented Numerics” – J. Belanger Elligno Inc. Technical Report no. TR-2016-01 (September 2016)
Abstract Over the last few years we have been migrating a small library of numerical code originally written in C to C++. In this report, we present the mathematical abstractions used and how object-oriented programming techniques are applied for scientific software design. Finally implementations details are provided including relationship between data structure. The result is tight, readable code that is easy to maintain and extend. Example with Shallow water equations is drawn from our prototype C++ based environment.
“Validating Shock Capturing Schemes On The Dam Break Problem” – J. Belanger, Elligno Inc. Technical report no. TR1-2007-01 (March 2007)
Abstract In this report we discuss some numerical techniques for approximating the Shallow-water equations. In particular finite difference schemes, adaptation of Roe’s approximate Riemann solver and the HLL scheme of (Harten-Lax-Van Leer) with the objective of accurately approximating the solution of Shallow-water equations over variable topography. Some tests are presented as preliminary validation of the proposed framework. Satisfactory comparisons have been obtained. This report shows progress towards a more complete validation of the schemes and demonstrate a critical need to improve procedure if such progress is to be sustained.
Presentation
“On the Development of a Scientific Programming Environment For The DamBreak Simulation”, MathWorks (MathLab Core Group), Boston, MA (USA) (September 2015)
Presented the programming environment that I have developed for the dam break simulation. This environment provides an easy way to program and test numerical scheme on the well-known DamBreak problem. I have presented the architecture of the framework and an example of how to program a numerical algorithm.
