Biotechnology Industry

R

Client: ART Inc.

Technologies: C++, OO, Matlab, gnuplot, VTK visualizing tool, programmation algorithme numérique, non-linear fit

Projet: Scientific Programmer in charge (molecular imaging)

Re-designed the curve fit library and implemented an Object-Oriented architecture, modular approach by developing an easy-to-use programming API (Application Program Interface). This updated version featured: efficient and robust optimization for fast floating-point operation, extensible class hierarchies that let user readily implement new algorithms.

Molecular Imaging Technology

Molecular imaging involves illuminating the part of the body of interest with non-ionizing radiation and analyzing the emergent pattern for signs of pathology (normal tissue differs from abnormal in its absorption or scattering properties). These techniques are well suited for the evaluation of the response to therapy in cancer to monitor their progression or treat medical conditions at a molecular level.

Solving Scattering/Absorption Coefficients Algorithm 

Scattering/absorption coefficients may be determined independently by fitting to the time-varying diffusion equation. The problem is to use some set of measurements (data obtained from the scanner) and choose a mathematical (curve fit) model to be fitted to the data. A nonlinear curve fitting is performed by solving an Optimization problem where an objective function is minimized (error minimization by Least Square which represents the error between the original data and the calculated fit) for a set of parameters. It starts with the initial guesses for the unknown parameters and at each iteration varies the parameter values slightly and re-evaluate Least Square until it finds the best fit.

Architecture API (OON: Object-Oriented Numerics)

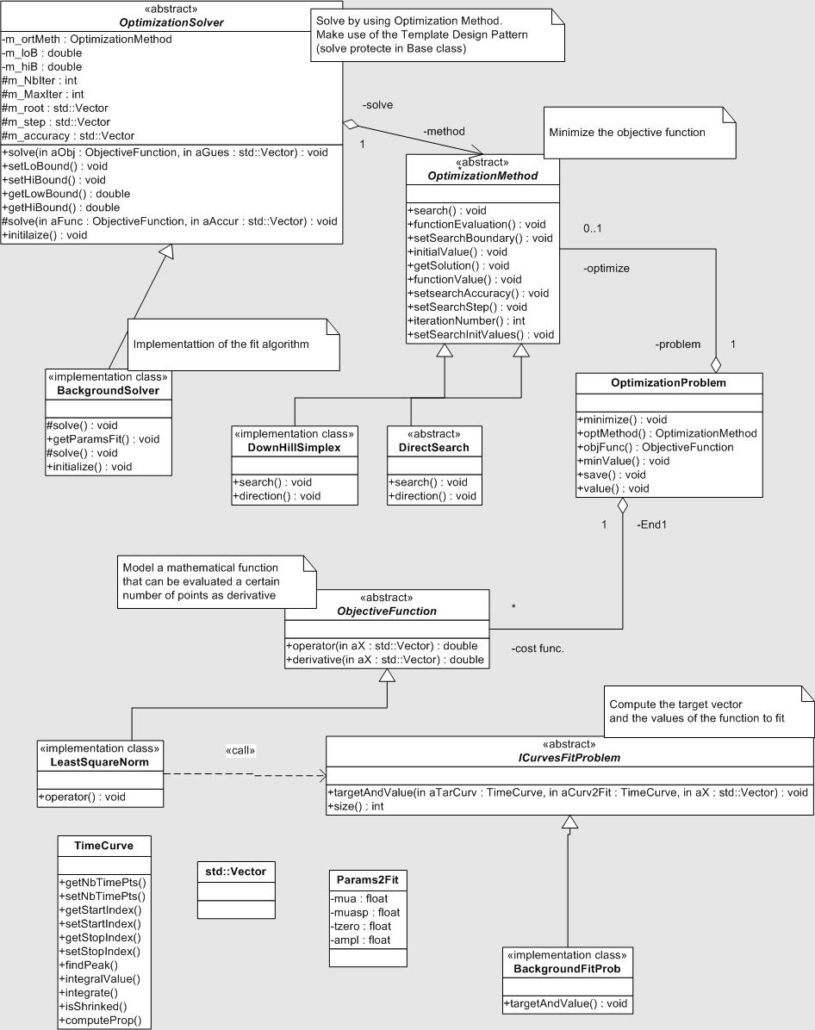
Object-Oriented Numerics was used for the implementation of the design, it is flexible tool that can be adapted to meet future requirements. OON and OOP (Object-Oriented Programming) are overlapping but not identical terms. The former encourages computer implementation of mathematical abstractions. UML diagrams are blueprints of architecture, the static class diagram below expresses top level abstractions or global concepts of the fit library ( set of mathematical abstractions), optimization problem by a numerical (optimization) method. 

Code Snippets

Top level class (abstract) which means we cannot instantiate. Provides basic services to solve an optimization problem (by some optimization method which is an attribute). The optimization method is pass as an argument to constructor (user have to create a method).

//Abstract Base Class for Curves Fitting Solver 
class OptimizationSolver {

  public:
      // Default ctor
      OptimizationSolver( std::vector<float> aVec, uint32 aMaxIter);
      OptimizationSolver( std::vector<float> aAccuracy, /*eps*/ uint32 aMaxIter, 
                          boost::shared_ptr&ltOptimizationMethod&gt aOpMeth);

      // Force destructor to be virtual
      virtual ~OptimizationSolver() {/*nothing to do*/}

      // Solve methods
      void solve( ObjectiveFunction & aFunc, std::vector<float> aGuess, std::vector<float> aStep) const;
      void solve( ObjectiveFunction & aFunc, std::vector<float> aGuess, std::vector<float> aMin, 
                  std::vector<float> aMax) const;

      // Boundary of the parameters
      void setLowBound( std::vector<float> aLowBound) { mLowBound = aLowBound;}
      void setHighBound( std::vector<float> aHighBound) { mHiBound = aHighBound;}
      std::vector<float> getLowBound() const { return mLowBound;}
      std::vector<float> getHighBound() const { return mHiBound;}

      // Initialize parameters .... and overwrited in the subclass
      virtual bool initialize( std::vector<float> aGuess, std::vector<float> aStep);

  protected:
      // Initial guess
      mutable std::vector<float> mRoot;
      mutable std::vector<float> mStep;

      // Required accuracy of the solver
      std::vector<float> mAccuracy;  // bestAccuracy_;
  
      // Maximum and real number of iterations
      unsigned int mMaxIterations;
      unsigned int mNbIterations;

      // Maximum and evaluation number of ....
      unsigned int mMaxEvaluations;
      mutable unsigned int mEvaluationNumber;

      // This method must be implemented in derived classes and contains the actual code which 
      // searches for the zeroes of the Objective Function. It assumes that:
      //  - xMin and xMax form a valid bracket
      //  - ... to be completed
      //  - mRoot was initialized to a valid initial guess
      virtual void solve( ObjectiveFunction & aFunc, std::vector<float> aAccuracy) const = 0;

      // Optimization method
      boost::shared_ptr&ltOptimizationMethod&gt mOptMeth;

  private:
      // Boundary value  
      std::vector<float> mLowBound;
      std::vector<float> mHiBound;

      // Boundary parameters almost fixed
      bool mLowBoundEnforced;
      bool mHiBoundEnforced;

      // Fix the lower and upper bounds of ...
      void enforcebounds( std::vector<float> aBounds) const;
};

Below inheriting class from the base class (depends on the fit algorithm choosen)

// "Model of" of the two-steps fitting algorithm. 
class TwoStepsFitSolver : public OptimizationSolver 
{
   public:
       // Set Direct Search algorithm as default Optimization Method
       TwoStepsFitSolver( std::vector<float> aAccuracy /*eps*/, uint32 aMaxIter, uint32 aNbParams);

       // Default ctor
       TwoStepsFitSolver( std::vector<float> aAccuracy /*eps*/, uint32 aMaxIter, uint32 aNbParams,
                          boost::shared_ptr&ltOptimizationMethod&gt aOptMeth);

       // Destructor
       ~TwoStepsFitSolver() {/*nothing to do*/}

       // Parameters of the fit
       inline ART::Data::BackGParams2Fit getParams2Fit() 
       {
           float* wResults = mOptMeth->GetSolution();
           mParams2Fit.mMua   = wResults[0];
           mParams2Fit.mMusp  = wResults[1];
           mParams2Fit.mAmpl  = wResults[2];
           mParams2Fit.mTzero = wResults[3];

           return mParams2Fit;
       }

       // Interface
       // Override solve method from base class
       void solve( ObjectiveFunction & aFunc, std::vector<float> aAccuracy) const;

       // Derived from base class
       bool initialize( std::vector<float> aGuess, std::vector<float> aStep);

   private:
       // Number of parameters for the fit
       unsigned int mNbParams2Fit;
       ART::Data::BackGParams2Fit mParams2Fit;
       // Store the result
       float* mResults;
};

Below model of a function using “called functor” in C++. More description coming

// Contini term structure function is the following  
//     T(rho, t) = exp()/2.(4piDv) Sum(......)
//
//     We evaluate the theoretical model, in this case we use the Contini Model.
//     Reference can be found in the following paper: 
//     "Photon Migration through a turbid slab described by a Model based
//      on Diffusion Approximation: I Theory", D. Contini, F. Martelli and G. Zaccanti
//     Applied Optics, Vol. 36, No.19 (Jul. 1997)
//
//  "Model of" functor
class ContiniFunction 
{
  public:
      // Default constructor to set coeffs
      ContiniFunction( float aCurrentMua, float aCurrentMusp, float aSpeedOfLight, float aThickness,
                       const ART::Data::Timing aTpsfTimeParams);
      // Operator to evaluate the function at given time
      ART::Data::FloatVec operator() ( float aRho, const float aTime);
      // Scale for ...
      void setScaleZb( float aScaleZb) { mScaledZB = aScaleZb;} 
   private:  
      // Coefficients of the function
      float mCurrentMua;
      float mCurrentMusp;
      float mSpeedOfLight;
      float mThickness;
      float mScaledZB;

      // Time parameters for the TPSF (Temporal ... Spread Function)
      ART::Data::Timing mTPSFTime;
};

Technical report “Background Fit Algorithm”, – J. Belanger, Technical Note ART Inc. (June 2005)