Environmental Industry
Shallow Water Simulation (Industrial Application: Sainte-Marguerite-3 (SM-3))
Environmental Industry: Hydro-Electricity
The role of computers in physics is growing in importance and there seems little doubt that this will accelerate. Today we are routinely solving problems that would be impossible to attack with the help of pen, paper and brain alone. The use of numerical methods to solve mathematical problems arising from a wide variety of applications has exploded in the last two decades or so. One major application is in the environmental industry. A key feature of numerical methods is that it makes it possible to theoretically model and simulate phenomena of interest. The flow in a river at different conditions may be simulated on the computer. That means that the key features of physical phenomena involved may be studied under a wide range of conditions by performing numerical simulations of the corresponding range of parameters values.
Sainte-Marguerite-3 (SM-3 ) Project
Project initiated from a collaborative work effort (University-Industry) for cautioning mathematical models in the hydraulics field (hydro-electricity production).
Main goal of the project is to establish a benchmark for validating numerical scheme in open channel flow simulation. The river reach selected (Sainte-Marguerite-3 (SM-3)) for the field test is a 2 km section and is located in the province of Quebec (Canada). This river reach was chosen for the complexity of its river flow and for the quality of the field data available. The reach exhibits torrential flow, transition to fluvial condition through a hydraulic jump, complex bed elevation including an island and flood plains.
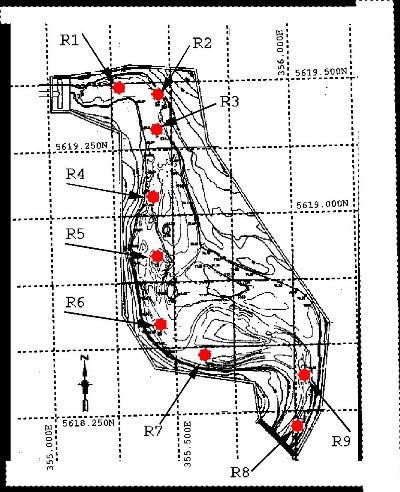
Context Simulation of river flow within the framework of a two-dimensional St-Venant model on a very complex bathymetry. We have the topographic data of the river as well as the Level-Discharge relationship curve for different flow regimes. Moreover, we have for a given flow regime (2500m3/s) the water level measured at different locations along the river marked as R1-9 red points (see picture last one at right far end).
Interpolation The precision will depend partly on the interpolation of the topographic data on the grid. Lot of effort has been made to interpolate data on the grid as close as possible. But we have adjusted as best we can (manual adjustment).
Calibration We have done simulations for adjusting model parameters to align with experimental data (empirical constants, Manning etc…) to minimize errors and improve accuracy.
A finite elements numerical scheme of the Galerkin type at order two was used. This corresponds to a central scheme. We impose Q(discharge) = 2500m3/s. upstream and a water height downstream (74.3m water level).
We have succeeded in reproducing a flow regime. However, we have problems obtaining results with an acceptable degree of precision (within 10cm of the terrain data).
SM-3 : Des essais techniques amorcés pour une 3e turbine (radio-canada.ca)

Figures below show (from left to right)
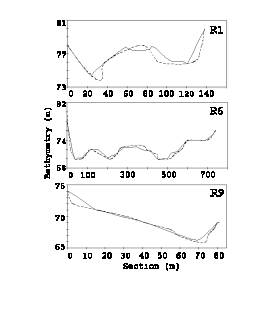
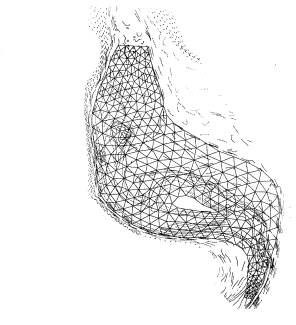
First, cross-section taken along different reference R points showing the strong sharp gradient in the bottom. The next image show the river basin network is represented by an unstructured grid system using six nodes triangular elements which are located to appropriately represent the flow regime. This element has satisfied all the tests of stability and precision for transient and steady state real life flows. Finally, topography map of the 2km river section. This map has been used to produce the network (mesh) and to adjust the bathymetry on the riverbanks.
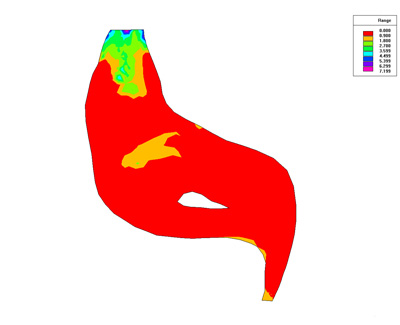
Below we present some result of the simulation. Numerical used is Finite Element of Galerkin type.
Simulation Results
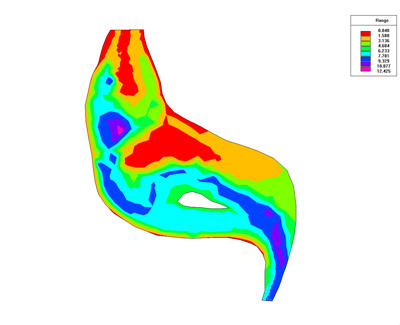
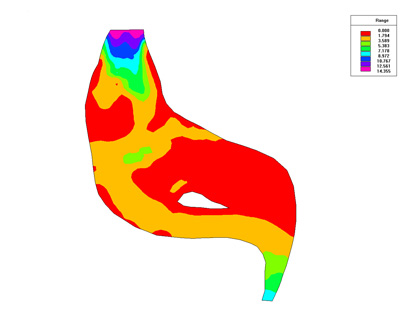
References
“A Test Field Calibration to Validate Shallow-Water Codes: the Case of the Ste- Marguerite River with AquaDyn”, J. Belanger, M. Carreau and A. Vincent CERCA Technical Report no. R2000-6, September 2000
“Simulation 2D d’une section de la riviere Ste-Marguerite” J. Belanger et A.Vincent Contract work under SoftKit Technologies Inc. and CERCA (1995)
Phd Thesis (not completed)
Abstract In the simulation of the flows with strong variations in the bottom topography, it is essential to integrate the discrete representation of each term with an acceptable degree of accuracy and stability. Improper treatment of these terms may lead to great inaccuracies if strong variations of the bottom topography are present. In this context recently published numerical algorithms pertaining to this problem as well as available experimental data have been used for purposes of validation of the present schemes. The case under consideration is well suited to study the influence of the numerical treatment of the pressure and bottom-slope terms, because of the complexity of the flow. I do believe that all forgoing works are particularly useful contributions to the numerical solution of the St-Venant equations and could be used as a benchmark to test new numerical solvers dedicated to flow conditions.
