Industrie Biotechnologie (Programmeur Scientifique)

Imagerie Moléculaire

Art est un chef de file dans les produits d’imagerie moléculaire optique pour les industries des soins de santé et pharmaceutique. Mandat à titre de programmeur scientifique (biotechnologie).

Client: ART Inc.

Technologies: C++, OO, Matlab, gnuplot, VTK visualizing tool, programmation algorithme numérique, non-linear fit et optimization,Orienté-Objet, STL, boost

Projet: Programmeur Scientifique biotechnologie en charge de la librairie mathématique

Technologie Imagerie Moléculaire

ART Advanced Research Technologies Inc. développe et commercialise des produits d’imagerie moléculaire pour les industries de la santé et pharmaceutique. L’imagerie moléculaire consiste à éclairer la partie du corps d’intérêt avec un rayonnement non ionisant et à analyser le motif émergent à la recherche de signes de pathologie. La tâche consiste à étudier à la fois les propriétés de diffusion et d’absorption des tissus, la manière dont la lumière se propage à travers les tissus (les tissus normaux diffèrent des tissus anormaux par leur absorption ou leur diffusion), il devient alors possible de différencier optiquement les conditions normales et anormales. Les techniques d’imagerie moléculaire sont bien adaptées à l’évaluation de la réponse au traitement du cancer. Cela permet aux médecins de scruter le corps vivant afin d’identifier des maladies, de surveiller leur progression ou de traiter des conditions médicales au niveau moléculaire.

Description

Solutionner équation de diffusion par méthode d’optimisation (problème d’optimisation) en utilisant un ajustement non linéaire. Dans cette approximation, la solution est modélisée par un modèle de données expérimental qui dépend de certains paramètres empiriques : les coefficients de diffusion et d’absorption. Ceux-ci peuvent être déterminés indépendamment par ajustement (non linéaire dans ce cas) à l’équation de diffusion variable dans le temps. Pour trouver les paramètres optimaux de l’ajustement, on fait appel à un problème d’optimisation. 

Mandat

Re-designer une librairie d’interpolation (lissage d’une courbe) en utilisant une approche modulaire de type API. Environnement qui permet d’ajouter de nouveaux algorithmes facilement avec un minimum d’effort.

J’ai mis en place une architecture orientée objet, une approche modulaire en développant une API de programmation facile à utiliser. Cette nouvelle version de la bibliothèque présentait : optimisation robuste pour le calcul à virgule flottante (deux fois plus rapide que la version originale), une hiérarchie qui permet d’implémenter facilement de nouveaux algorithmes. Accélère la phase de prototypage de nouveaux algorithmes numériques de fit ainsi que la gestion de développement futur

Architecture API

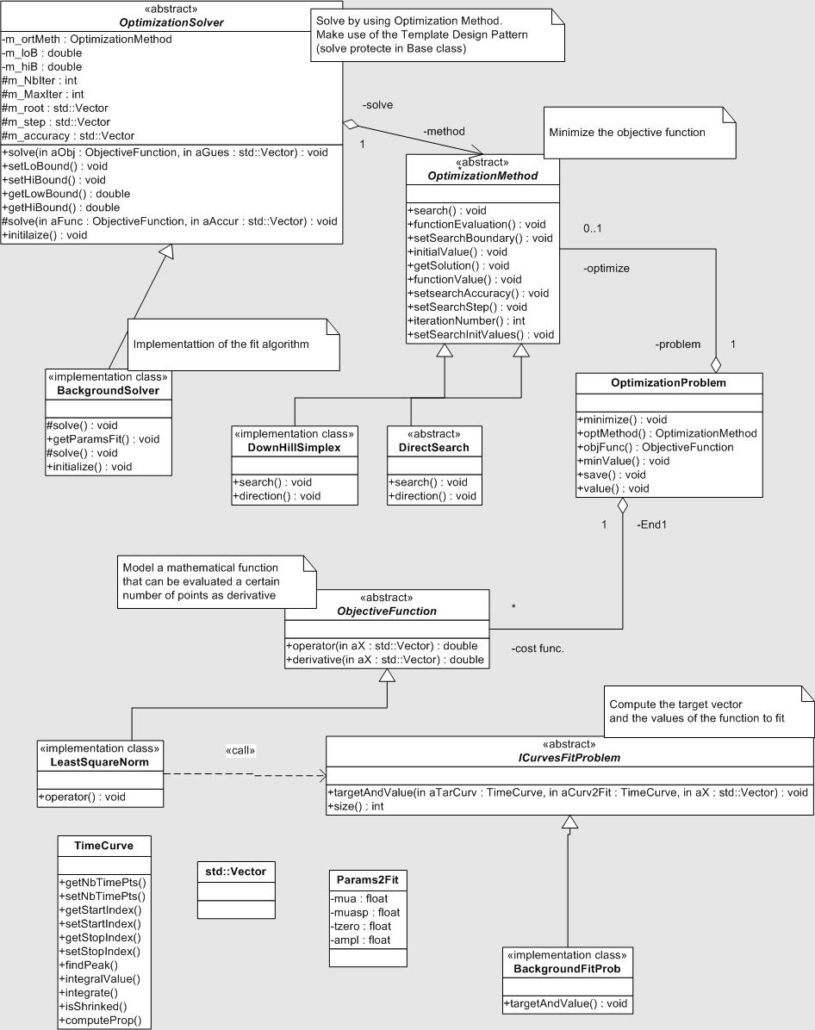
Ci-dessous diagramme UML (Unified Modeling Language) de l’API de la bibliothèque numérique. Le diagramme de class montre la dépendance entre les types, un portrait global de l’architecture.

Hiérarchie de class (type de base) afin de fournir des services de base pour la programmation de nouveaux algorithmes pour résoudre le problème d’optimisation. L’utilisateur doit implémenter les services de la ‘class’ de base pour ses besoins particuliers. De cette façon, l’algorithme principale fait appel aux services de la ‘class’ de haut niveau, indépendant des différentes implémentations. Ainsi on évite de modifier l’algorithme principale de l’application par des détails d’implémentations, donc plus facile à maintenir, les changements sont localisés.

Exemple de Code

Presente quelques exemples de code et de programmation d’algorithme.

class OptimizationSolver {

  public:
      // Default ctor
      OptimizationSolver( std::vector<float> aVec, uint32 aMaxIter);
      OptimizationSolver( std::vector<float> aAccuracy, /*eps*/ uint32 aMaxIter, 
                          std::shared_ptr<OptimizationMethod> aOpMeth);

      // Force destructor to be virtual
      virtual ~OptimizationSolver()=default;

      // Solve methods
      void solve( ObjectiveFunction & aFunc, std::vector<float> aGuess, std::vector<float> aStep) const;
      void solve( ObjectiveFunction & aFunc, std::vector<float> aGuess, std::vector<float> aMin, 
                  std::vector<float> aMax) const;

      // Boundary of the parameters
      void setLowBound( std::vector<float> aLowBound) { mLowBound = aLowBound;}
      void setHighBound( std::vector<float> aHighBound) { mHiBound = aHighBound;}
      std::vector<float> getLowBound() const { return mLowBound;}
      std::vector<float> getHighBound() const { return mHiBound;}

      // Initialize parameters .... and overwrited in the subclass
      virtual bool initialize( std::vector<float> aGuess, std::vector<float> aStep);

  protected:
      // Initial guess
      mutable std::vector<float> mRoot;
      mutable std::vector<float> mStep;

      // Required accuracy of the solver
      std::vector<float> mAccuracy;  // bestAccuracy_;
  
      // Maximum and real number of iterations
      unsigned int mMaxIterations;
      unsigned int mNbIterations;

      // Maximum and evaluation number of ....
      unsigned int mMaxEvaluations;
      mutable unsigned int mEvaluationNumber;

      // This method must be implemented in derived classes and contains the actual code which 
      // searches for the zeroes of the Objective Function. It assumes that:
      //  - xMin and xMax form a valid bracket
      //  - mRoot was initialized to a valid initial guess
      virtual void solve( ObjectiveFunction & aFunc, std::vector<float> aAccuracy) const = 0;

      // Optimization method
      boost::shared_ptr<OptimizationMethod> mOptMeth;

  private:
      // Boundary value  
      std::vector<float> mLowBound;
      std::vector<float> mHiBound;

      // Boundary parameters almost fixed
      bool mLowBoundEnforced;
      bool mHiBoundEnforced;

      // Fix the lower and upper bounds of ...
      void enforcebounds( std::vector<float> aBounds) const;
};